Diện Tích Hình Thang là dạng bài quen thuộc trong hình học nhưng lại rất dễ sai nếu nhầm đáy, nhầm chiều cao hoặc quên đổi đơn vị. Khi nắm đúng công thức và biết cách xác định “h” trong từng tình huống, bạn sẽ giải nhanh từ bài cơ bản đến bài có dữ kiện ẩn. Bài viết dưới đây tổng hợp công thức chuẩn, lưu ý thường gặp và một vài mở rộng giúp bạn tự tin hơn khi làm bài.
Diện Tích Hình Thang: Công thức cơ bản dễ nhớ
Nhận diện đúng đáy lớn, đáy bé và chiều cao
Trong hình thang, hai cạnh song song được gọi là hai đáy (thường ký hiệu a và b), còn đoạn thẳng vuông góc nối từ đáy này sang đáy kia là chiều cao h. Nhiều bạn nhìn hình vẽ xoay chiều rồi chọn nhầm “đáy” thành cạnh bên, dẫn đến đặt sai dữ kiện ngay từ bước đầu. Để tránh nhầm, hãy luôn kiểm tra: đáy phải là hai cạnh song song.
Một mẹo nhận diện nhanh là kẻ (hoặc tưởng tượng) một đường thẳng vuông góc từ một đỉnh trên xuống đáy dưới để thấy rõ chiều cao. Chiều cao không nhất thiết nằm bên trong hình nếu hình thang bị “lệch”, nhưng bản chất vẫn là khoảng cách giữa hai đường thẳng chứa hai đáy. Khi xác định được h, phần còn lại chủ yếu là thay số và tính toán cẩn thận.
Công thức tính và cách biến đổi linh hoạt
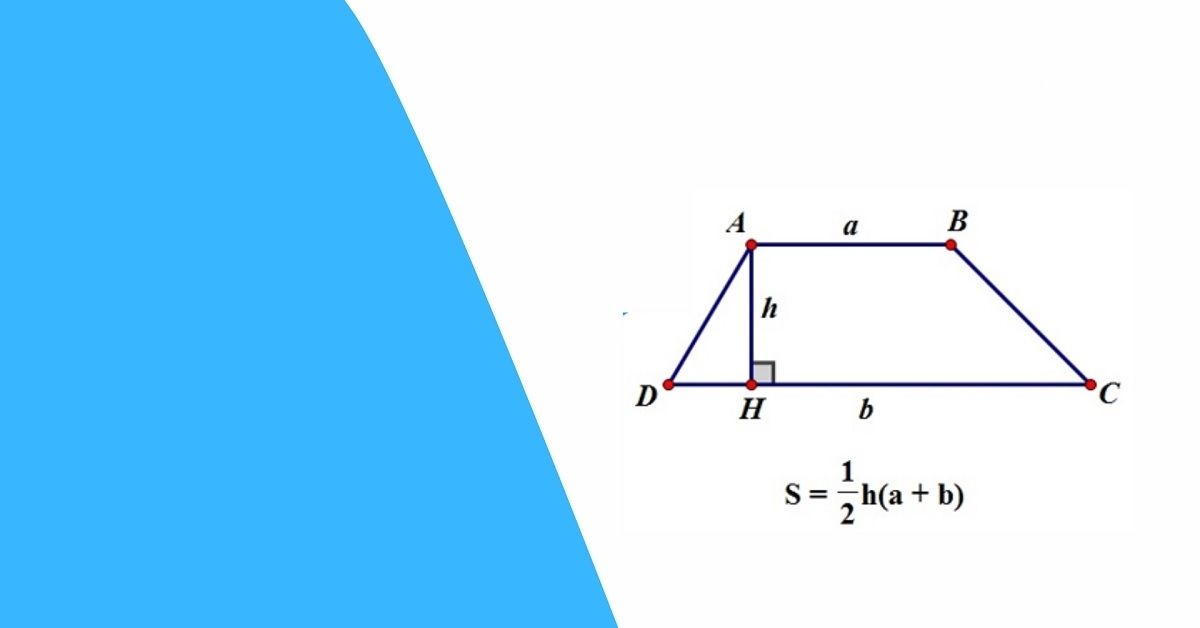
Công thức chuẩn để tính diện tích là: S = (a + b) × h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao. Ý nghĩa của công thức này có thể hiểu như “diện tích bằng chiều cao nhân với trung bình cộng của hai đáy”. Chỉ cần nhớ đúng ba yếu tố (hai đáy song song và chiều cao vuông góc) là bạn sẽ áp dụng được cho hầu hết bài toán.
Khi gặp bài yêu cầu tìm một đại lượng còn thiếu, bạn chỉ cần biến đổi công thức như với phép toán đại số thông thường. Ví dụ, nếu biết S và hai đáy, ta suy ra h = 2S / (a + b). Nếu biết S, h và một đáy, ta tìm đáy còn lại bằng cách đưa ẩn về một phía rồi giải đơn giản, tránh nhảy bước khiến sai dấu hoặc sai thứ tự phép tính.
Diện Tích Hình Thang: Các trường hợp đặc biệt và mở rộng
Hình thang vuông: dễ tìm chiều cao nhưng vẫn có “bẫy”
Với hình thang vuông, một cạnh bên vuông góc với hai đáy nên cạnh đó chính là chiều cao. Nhờ vậy, bạn thường không cần kẻ thêm đường phụ mà có thể thay số trực tiếp vào công thức. Tuy nhiên, “bẫy” hay gặp là nhiều đề cho cạnh bên còn lại hoặc cho đường chéo, khiến bạn vội lấy nhầm làm h.
Nếu đề bài không cho trực tiếp cạnh vuông mà cho độ dài cạnh bên và độ lệch giữa hai đáy, bạn có thể phải dùng định lý Pythagore để tìm chiều cao. Khi đó, hãy tách hình thang thành một hình chữ nhật và một tam giác vuông (bằng cách hạ đường cao) để nhìn ra các cạnh liên hệ. Làm chậm ở bước dựng hình sẽ giúp bạn tiết kiệm rất nhiều thời gian tính toán về sau.
Dùng trung bình cộng hai đáy để tính nhanh
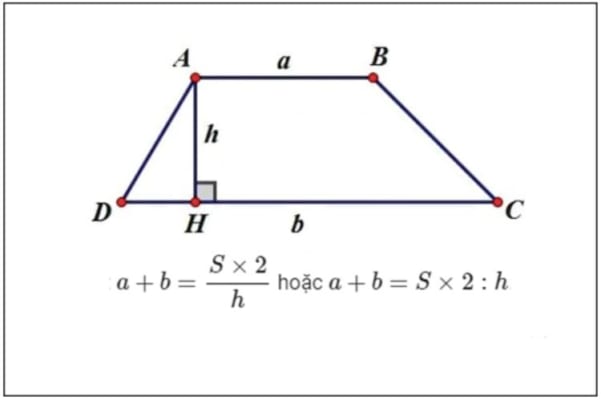
Một cách trình bày gọn là đặt m = (a + b)/2 (m chính là “đáy trung bình” theo nghĩa trung bình cộng), khi đó S = m × h. Cách này đặc biệt hữu ích khi a và b là phân số hoặc số thập phân, vì bạn có thể rút gọn m trước rồi mới nhân với h. Nhờ đó, phép tính cuối cùng thường gọn hơn và ít sai sót hơn.
Trong nhiều bài hình học nâng cao, đề có thể cho “độ dài đường trung bình” (đoạn nối trung điểm hai cạnh bên) và cho chiều cao, rồi yêu cầu tính diện tích. Khi đó, bạn chỉ cần nhớ: đường trung bình của hình thang có độ dài bằng (a + b)/2, tức là đúng bằng m. Đây là cầu nối quan trọng giữa dữ kiện hình học và phép tính diện tích.
Suy ngược dữ kiện: khi biết diện tích để tìm đáy hoặc chiều cao
Không ít bài toán cho diện tích rồi yêu cầu tìm một đáy khi đã biết đáy còn lại và chiều cao. Lúc này, bạn nên viết công thức ra giấy, thay các giá trị đã biết, và để ẩn ở vị trí dễ quan sát (thường là đặt ẩn là a hoặc b). Sau đó, nhân chéo và rút gọn từng bước để tránh sai số, nhất là khi có phân số.
Với dạng bài “tăng/giảm một đáy” hoặc “thay đổi chiều cao” mà diện tích thay đổi theo, bạn nên so sánh theo công thức S = (a + b) × h / 2. Nếu chỉ đổi một đáy thêm k, thì diện tích tăng thêm k × h / 2; nếu chỉ đổi chiều cao thêm t, thì diện tích tăng thêm (a + b) × t / 2. Cách nhìn này giúp bạn giải nhanh bài toán thực tế mà không cần dựng lại hình.
Diện Tích Hình Thang: Lưu ý quan trọng khi áp dụng công thức
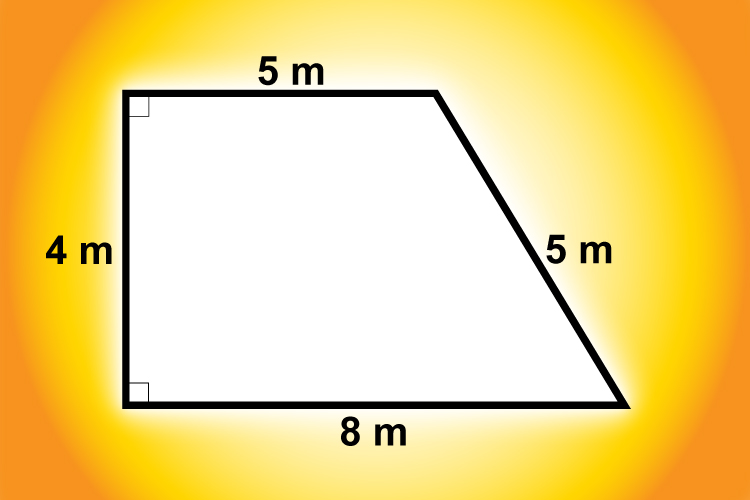
Đổi đơn vị đo trước khi tính
Sai lầm phổ biến là thay số khi các đại lượng đang khác đơn vị, chẳng hạn đáy tính theo cm nhưng chiều cao tính theo m. Trước khi bấm máy, hãy quy về cùng một hệ đơn vị (thường là cm hoặc m) để phép nhân và phép chia có ý nghĩa đúng. Việc đổi đơn vị xong mới tính sẽ giúp bạn tránh sai lệch kết quả lên tới hàng chục, hàng trăm lần.
Ngoài ra, hãy để ý đề bài yêu cầu đơn vị kết quả là gì: cm², m² hay ha (hecta) trong bài toán diện tích đất. Khi đổi từ đơn vị độ dài sang đơn vị diện tích, bạn phải bình phương hệ số đổi (ví dụ 1 m = 100 cm thì 1 m² = 10.000 cm²). Chỉ một bước quên bình phương cũng đủ khiến đáp án sai hoàn toàn.
Xác định đúng chiều cao trong hình vẽ nghiêng
Chiều cao là khoảng cách giữa hai đường thẳng chứa hai đáy, nên nó luôn vuông góc với đáy. Nếu hình thang nghiêng, đoạn thẳng bạn nhìn thấy “gần giống” vuông góc đôi khi chỉ là cạnh bên, không phải chiều cao. Cách chắc chắn nhất là kẻ đường cao từ một đỉnh xuống đáy còn lại và dùng dấu vuông góc để xác nhận.
Nếu đề cho đường chéo, cạnh bên, hoặc góc, bạn có thể phải dùng tam giác vuông phụ để tính h trước khi tính diện tích. Hãy ưu tiên dựng hình thành các tam giác vuông quen thuộc để áp dụng Pythagore hoặc lượng giác cơ bản. Khi tìm được h rồi, việc tính diện tích chỉ còn là thay vào công thức và rút gọn.
Tránh nhầm đáy với cạnh bên khi đề bài “đổi hướng” hình
Đề bài có thể xoay hình thang theo nhiều hướng: đáy lớn ở dưới, ở trên, hoặc ở bên trái/phải. Dù hình xoay thế nào, hai đáy vẫn là hai cạnh song song, còn hai cạnh còn lại là cạnh bên. Bạn nên rà lại bằng cách dùng thước thẳng tưởng tượng kéo dài hai cạnh xem chúng có cắt nhau không; nếu không cắt, đó mới là cặp đáy.
Một lỗi khác là nhầm “độ dài đường cao” với “độ dài cạnh bên” khi hình thang không vuông. Chỉ khi cạnh bên vuông góc với đáy thì nó mới trùng với chiều cao. Vì vậy, hãy tìm dấu hiệu vuông góc hoặc dữ kiện cho phép suy ra vuông góc trước khi kết luận.
Diện Tích Hình Thang: Ví dụ minh họa và mẹo kiểm tra nhanh
Ví dụ 1: Thay số trực tiếp theo công thức
Cho hình thang có đáy lớn a = 12 cm, đáy bé b = 8 cm, chiều cao h = 5 cm. Ta tính S = (12 + 8) × 5 / 2 = 20 × 5 / 2 = 50 cm². Khi trình bày, bạn nên ghi rõ bước cộng hai đáy, nhân với chiều cao, rồi chia 2 để tránh bị trừ điểm vì thiếu lập luận.
Nếu bạn muốn kiểm tra nhanh, hãy tính trung bình cộng hai đáy là (12 + 8)/2 = 10, rồi nhân với h = 5 để được 50. Hai cách phải cho ra cùng một kết quả, nhờ đó bạn phát hiện sớm lỗi bấm máy hoặc lỗi nhầm phép chia. Đây là thói quen tốt khi làm bài thi trắc nghiệm.
Ví dụ 2: Tìm chiều cao rồi mới tính diện tích
Giả sử hình thang vuông có hai đáy lần lượt 14 cm và 6 cm, cạnh bên nghiêng dài 10 cm, còn độ lệch giữa hai đáy là 8 cm. Hạ đường cao sẽ tạo tam giác vuông có cạnh huyền 10 cm và cạnh đáy 8 cm, nên chiều cao h = √(10² − 8²) = √(100 − 64) = 6 cm. Khi đã có h, bạn áp dụng công thức diện tích như bình thường để ra kết quả.
Cách làm này cho thấy một điểm quan trọng: đôi khi bài không cho sẵn chiều cao mà “giấu” trong một tam giác vuông. Nếu bạn vội thay số mà chưa tìm đúng h, bạn sẽ đi sai ngay từ đầu. Vì thế, luôn kiểm tra xem dữ kiện đã đủ ba yếu tố (hai đáy và chiều cao) hay chưa trước khi tính.
Mẹo tự kiểm tra kết quả trong 10 giây
Để kiểm tra nhanh, hãy ước lượng: diện tích hình thang phải nằm giữa diện tích của hai hình chữ nhật có đáy lần lượt là a và b cùng chiều cao h. Nghĩa là b×h < S < a×h nếu a > b và h > 0, giúp bạn phát hiện kết quả “quá lớn” hoặc “quá nhỏ” ngay lập tức. Với cách này, bạn không cần tính lại từ đầu mà vẫn có thể phát hiện lỗi sai thường gặp.
Bạn cũng có thể kiểm tra bằng việc hoán đổi a và b; do công thức dùng (a + b), kết quả không đổi nếu đổi vị trí hai đáy. Nếu đáp án của bạn thay đổi khi bạn đổi a và b, chắc chắn bạn đã nhầm công thức hoặc nhầm dữ kiện. Đây là mẹo rất hữu ích khi bạn đang làm bài dưới áp lực thời gian.
Diện Tích Hình Thang: Ứng dụng thực tế dễ gặp
Tính diện tích bề mặt trong đời sống
Trong thực tế, nhiều mặt cắt của vật thể có thể gần giống hình thang: mái nhà dốc, miếng kính, mặt cắt mương thoát nước, hoặc miếng gỗ được cắt vát. Khi đo đạc, bạn thường xác định hai cạnh song song và khoảng cách giữa chúng, sau đó áp dụng công thức diện tích. Cách làm này giúp ước tính vật liệu cần dùng hoặc chi phí thi công tương đối chính xác.
Khi áp dụng cho đo đạc ngoài thực địa, bạn cần chú ý sai số đo và đơn vị. Nếu dùng thước mét và đo được số thập phân, hãy làm tròn hợp lý theo yêu cầu (ví dụ làm tròn đến 0,01 m) trước khi nhân chia. Sai số nhỏ ở độ dài có thể tạo ra sai số lớn ở diện tích nếu bạn không kiểm soát tốt bước làm tròn.
Liên hệ với cắt ghép hình học để hiểu bản chất
Một cách hiểu bản chất là tưởng tượng cắt và ghép hai hình thang bằng nhau để tạo thành hình bình hành có đáy là (a + b) và chiều cao là h. Khi đó, diện tích hình bình hành là (a + b)×h, nên diện tích một hình thang bằng một nửa, tức là (a + b)×h/2. Cách suy luận này không chỉ giúp bạn nhớ công thức lâu hơn mà còn giúp giải thích “vì sao phải chia 2”.
Nếu bạn học tiếp lên các lớp cao hơn, tư duy cắt ghép còn giúp bạn xử lý bài toán có hình phức tạp bằng cách chia nhỏ thành các hình quen thuộc. Khi biết cách chuyển đổi giữa hình chữ nhật, tam giác, hình bình hành và hình thang, bạn sẽ linh hoạt hơn rất nhiều. Điều quan trọng là luôn giữ đúng khái niệm chiều cao và cặp cạnh song song bên cạnh xemayanhloc.
Kết luận
Khi hiểu rõ hai đáy song song và chiều cao vuông góc, Diện Tích Hình Thang sẽ trở thành dạng bài “ăn điểm” nhờ công thức ngắn gọn và dễ biến đổi. Hãy luôn đổi đơn vị trước khi tính, xác định đúng h trong hình nghiêng, và dùng mẹo ước lượng để tự kiểm tra kết quả. Luyện thêm vài ví dụ suy ngược dữ kiện sẽ giúp bạn chắc tay với cả bài cơ bản lẫn bài nâng cao.
Trâm Anh là tác giả chính của trang web Xe Máy Anh Lộc . Với ngòi bút sắc sảo và am hiểu sâu về xe máy, cô chuyên viết review chi tiết, đánh giá xe cũ, hướng dẫn mua bán, tập trung vào các dòng tay ga phổ biến như Honda SH, Air Blade, Liberty. Nội dung thực tế, hữu ích, giúp người đọc đưa ra quyết định sáng suốt.
