Công Thức Lượng Giác là nhóm đẳng thức giúp bạn biến đổi biểu thức và giải các bài toán có sin, cos, tan theo cách bài bản. Khi học theo nhóm công thức và hiểu “dấu hiệu nhận dạng” trong đề, bạn sẽ rút gọn nhanh hơn và tránh sai dấu ở những bước quan trọng.
Công Thức Lượng Giác là gì và dùng khi nào?
Những tình huống hay gặp trong đề thi
Bạn cần công thức khi biểu thức xuất hiện góc dạng x ± a, 2x ± a, hoặc có tích/lũy thừa của sin, cos khiến việc rút gọn trở nên rối. Trong phương trình, công thức giúp đưa các hạng tử về cùng dạng để đặt ẩn phụ, tách nhân tử, hoặc đối chiếu điều kiện xác định trước khi kết luận nghiệm.
Cách học theo nhóm để không bị rối
Thay vì học rời rạc, hãy chia theo nhiệm vụ: hệ thức cơ bản, cộng–trừ góc, nhân đôi–góc nửa, hạ bậc, và đổi tích–tổng. Mỗi nhóm gắn với một tín hiệu: thấy sin²/cos² thì nghĩ hạ bậc, thấy x ± a thì ưu tiên cộng–trừ, thấy tích khác góc thì nghĩ đổi tích thành tổng để gom hạng tử.
Hệ thức lượng giác cơ bản cần nắm chắc
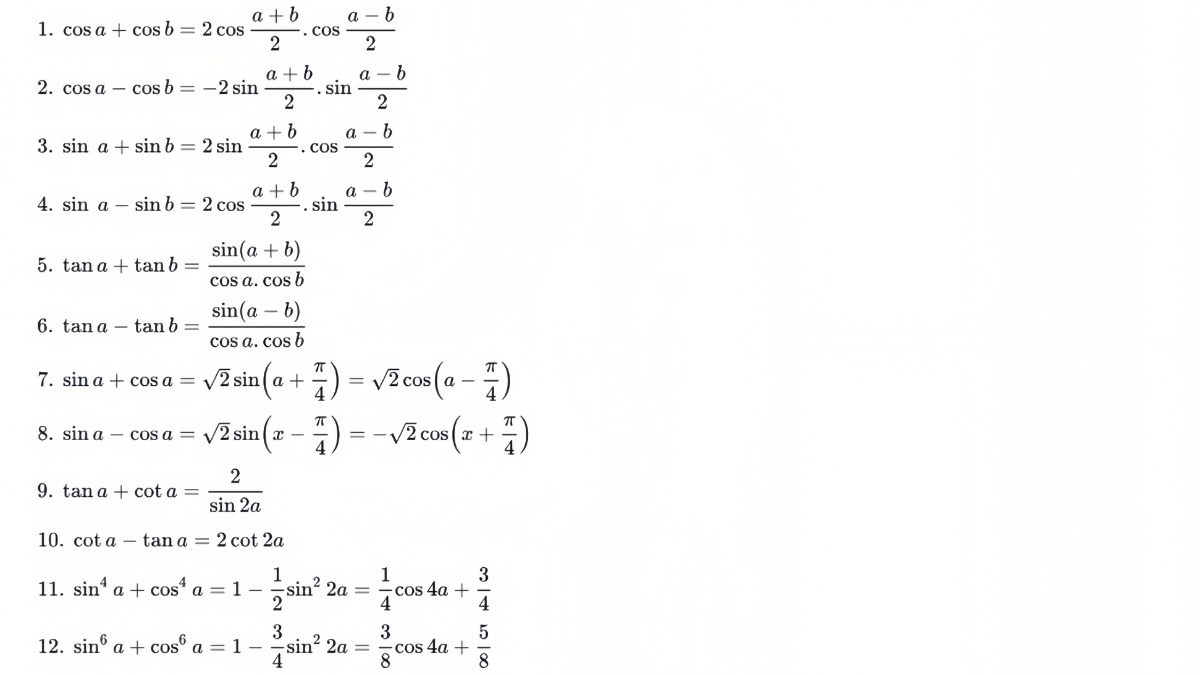
Ba hệ thức nền tảng
Đây là phần “xương sống” vì nhiều biến đổi chỉ là hệ quả của sin² + cos² = 1 và các phép chia hợp lệ theo điều kiện mẫu khác 0. Khi làm bài, nhóm này còn giúp bạn kiểm tra nhanh đáp án có hợp lý hay không, nhất là với các câu tính giá trị và chứng minh.
sin^2 x + cos^2 x = 1
1 + tan^2 x = 1 / cos^2 x
1 + cot^2 x = 1 / sin^2 x
Từ sin, cos suy ra tan, cot
Khi đề cho sin x hoặc cos x, bạn nên đổi tan và cot theo định nghĩa để tránh biến đổi lòng vòng. Luôn chú ý điều kiện cos x ≠ 0 hoặc sin x ≠ 0, vì nhiều bài phương trình có nghiệm “đẹp” nhưng lại làm mẫu bằng 0 nên phải loại.
tan x = sin x / cos x (cos x ≠ 0)
cot x = cos x / sin x (sin x ≠ 0)
Công thức cộng, trừ góc: xử lý x ± a
Sin, cos của tổng và hiệu
Nhóm cộng–trừ xuất hiện dày trong các biểu thức có x ± a và khi bạn cần tách một góc về các góc quen thuộc. Để hạn chế nhầm dấu, hãy nhớ sin giữ dấu (±) còn cos đổi dấu ở hạng tử sin·sin (∓), và luôn viết theo khuôn trước khi thay số.
sin(a ± b) = sin a cos b ± cos a sin b
cos(a ± b) = cos a cos b ∓ sin a sin b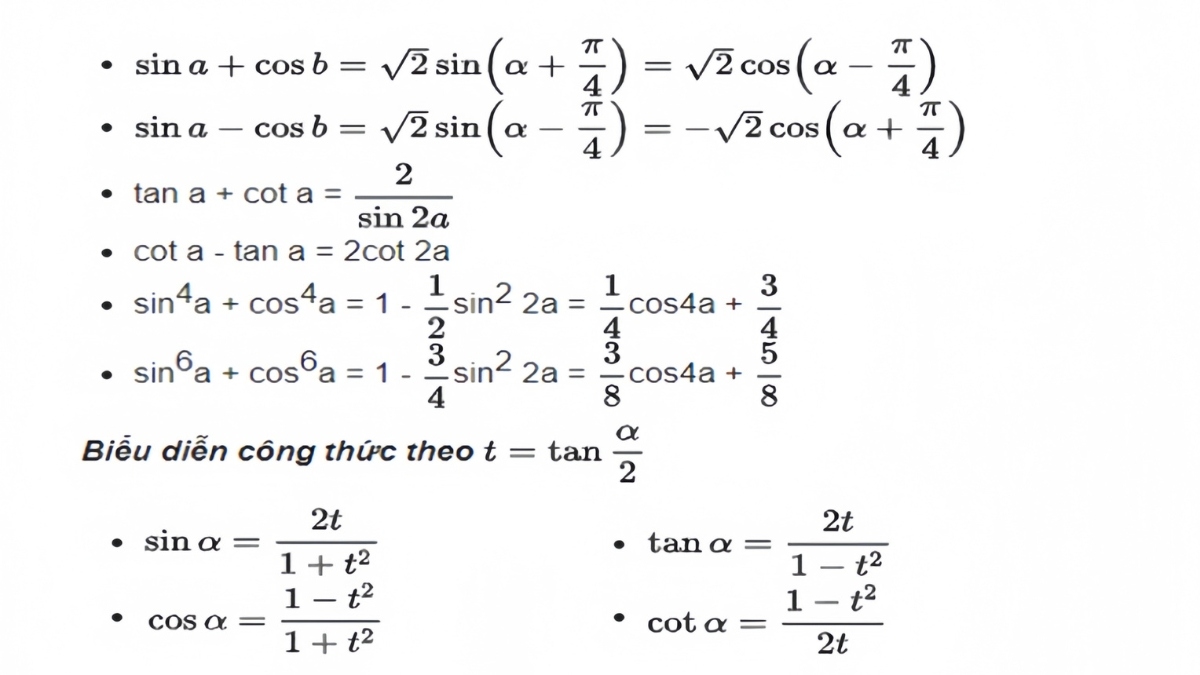
Tan của tổng và hiệu
Công thức tan(a ± b) mạnh khi biểu thức đã ở dạng phân thức chứa tan hoặc khi bạn muốn quy hết về một hàm để rút gọn nhanh. Khi giải phương trình, hãy kiểm tra điều kiện 1 ∓ tan a tan b ≠ 0 trước, vì bỏ qua điều kiện này dễ dẫn đến kết luận sai.
tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a tan b)
Nhân đôi và góc nửa: cầu nối giữa x và 2x
Nhân đôi với nhiều dạng của cos 2x
Khi gặp sin 2x hoặc cos 2x, bạn thường đổi về sin x và cos x để đặt ẩn hoặc tách nhân tử thuận lợi hơn. Riêng cos 2x có nhiều dạng tương đương, nên hãy chọn dạng khớp dữ kiện: theo sin² nếu đề cho sin, và theo cos² nếu đề cho cos.
sin 2x = 2 sin x cos x
cos 2x = 1 − 2 sin^2 x = 2 cos^2 x − 1
Góc nửa và cách chọn dấu
Góc nửa hữu ích khi bạn muốn chuyển cos x sang biểu thức theo sin(x/2), cos(x/2) để tính giá trị hoặc biến đổi về dạng chuẩn. Dấu ± không chọn tùy ý mà phụ thuộc vào miền giá trị của (x/2), vì sin và cos đổi dấu theo từng góc phần tư.
sin^2(x/2) = (1 − cos x) / 2
cos^2(x/2) = (1 + cos x) / 2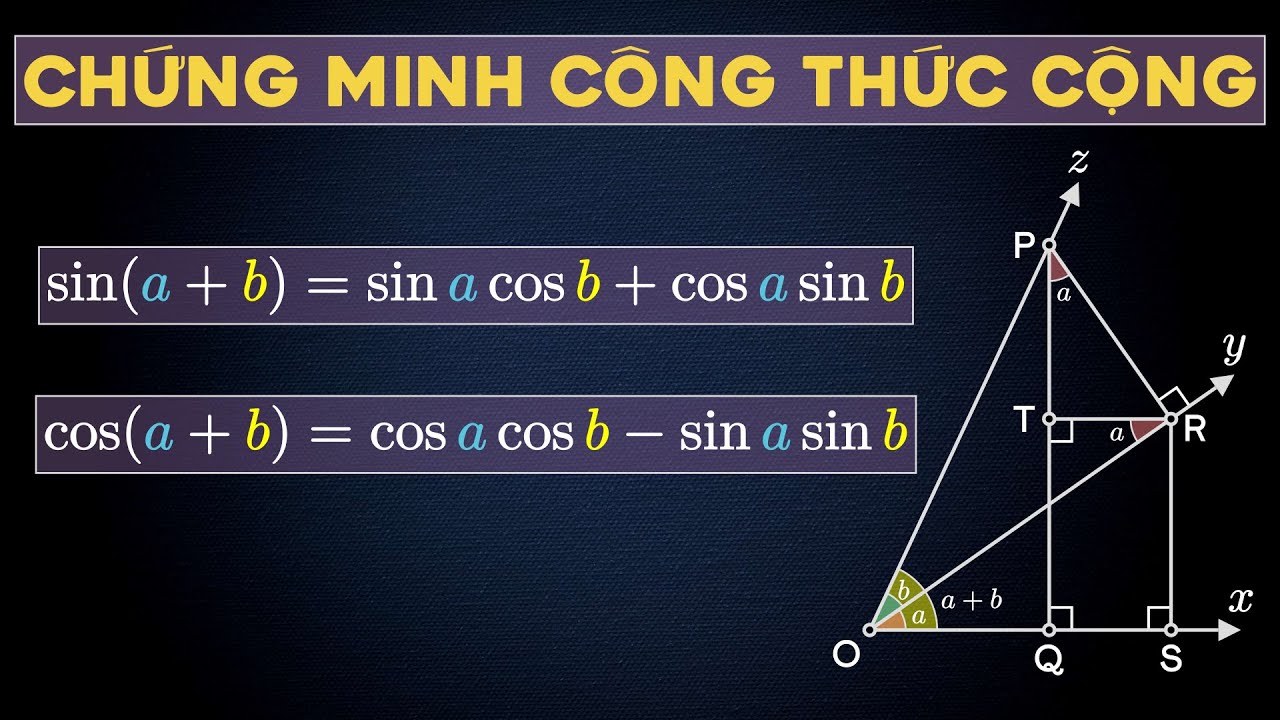
Hạ bậc và lũy thừa: rút gọn sin², cos²
Hạ bậc bậc hai
Nếu biểu thức có sin² x, cos² x mà bạn cần rút gọn hoặc so sánh, hạ bậc sẽ tạo ra cos 2x để gom hạng tử nhanh. Đây là bước rất “ăn điểm” trong các câu chứng minh và tính giá trị, vì sau hạ bậc bạn thường đưa được về tổng–hiệu quen thuộc.
sin^2 x = (1 − cos 2x) / 2
cos^2 x = (1 + cos 2x) / 2
Mẹo cho lũy thừa bậc lẻ
Với sin³ x hoặc cos³ x, cách làm gọn là tách một thừa số sin x hoặc cos x, phần còn lại đưa về bậc hai rồi hạ bậc. Ví dụ sin³ x = sin x·sin² x và thay sin² x theo (1 − cos 2x)/2 để tiếp tục rút gọn, nhờ vậy bạn không cần thuộc thêm công thức bậc ba riêng.
Đổi tích–tổng và mẹo biến đổi nhanh
Đổi tích thành tổng
Khi gặp tích như sin a·cos b hoặc cos a·cos b, đổi tích thành tổng giúp bạn đưa biểu thức về tổng các sin/cos để triệt tiêu hoặc rút gọn theo cặp. Sau khi đổi, hãy ưu tiên sắp xếp các hạng tử cùng dạng (cùng sin hoặc cùng cos) để nhìn ra bước tiếp theo.
sin a cos b = 1/2[sin(a + b) + sin(a − b)]
cos a cos b = 1/2[cos(a + b) + cos(a − b)]
sin a sin b = 1/2[cos(a − b) − cos(a + b)]
Đổi tổng thành tích và kiểm tra điều kiện
Nếu đề yêu cầu phân tích nhân tử hoặc đưa về tích để suy ra nghiệm, đổi tổng thành tích sẽ làm “lộ” thừa số chung theo (a + b)/2 và (a − b)/2. Sau khi biến đổi, hãy quay lại kiểm tra điều kiện xác định (đặc biệt khi có tan/cot hoặc mẫu số) để tránh giữ lại nghiệm không hợp lệ.
sin a + sin b = 2 sin((a + b)/2) cos((a − b)/2)
cos a + cos b = 2 cos((a + b)/2) cos((a − b)/2)
cos a − cos b = −2 sin((a + b)/2) sin((a − b)/2)
Khi bạn luyện nhận dạng “hình dạng” biểu thức (x ± a, sin²/cos², tích khác góc) và gắn đúng nhóm công thức, tốc độ làm bài sẽ tăng rõ rệt. Nếu nhóm hóa và luyện đều các dạng rút gọn, chứng minh, phương trình, Công Thức Lượng Giác sẽ trở thành chuỗi liên kết logic dễ nhớ thay vì danh sách dài khó thuộc.
Trâm Anh là tác giả chính của trang web Xe Máy Anh Lộc . Với ngòi bút sắc sảo và am hiểu sâu về xe máy, cô chuyên viết review chi tiết, đánh giá xe cũ, hướng dẫn mua bán, tập trung vào các dòng tay ga phổ biến như Honda SH, Air Blade, Liberty. Nội dung thực tế, hữu ích, giúp người đọc đưa ra quyết định sáng suốt.
