Công Thức Đạo Hàm là bộ quy tắc giúp bạn tính nhanh đạo hàm mà không phải quay lại định nghĩa giới hạn ở mỗi bài. Khi nắm chắc công thức và điều kiện áp dụng, bạn sẽ làm gọn các dạng tiếp tuyến, đơn điệu, cực trị và tối ưu hóa. Nội dung dưới đây hệ thống theo “nhóm hàm” và “nhóm quy tắc”, kèm ví dụ để bạn tự đối chiếu kết quả.
Công Thức Đạo Hàm: khái niệm và ký hiệu
Ý nghĩa của đạo hàm trong bài toán
Về mặt trực giác, đạo hàm tại (x_0) là hệ số góc tiếp tuyến của đồ thị tại điểm đó, nên nó cho biết hàm đang tăng hay giảm và tăng/giảm nhanh cỡ nào. Nếu cần nền tảng chặt chẽ, bạn nhớ định nghĩa (\displaystyle f'(x_0)=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}) khi giới hạn tồn tại. Khi hàm không trơn hoặc không xác định tại điểm xét, bạn phải loại điểm đó ra trước khi kết luận.
Ký hiệu và thói quen trình bày chuẩn
Bạn sẽ gặp (f'(x)), (y’) hoặc (\dfrac) và có thể dùng thống nhất một kiểu để bài giải mạch lạc. Khi gặp hàm hợp, hãy đặt (u=g(x)) rồi viết (y=f(u)) để nhìn rõ “vỏ–ruột”, tránh quên nhân (u’). Thói quen ghi miền xác định ngay sau khi đặt hàm sẽ giúp bạn không bỏ sót khoảng khi lập bảng biến thiên.
Công Thức Đạo Hàm cơ bản theo nhóm hàm
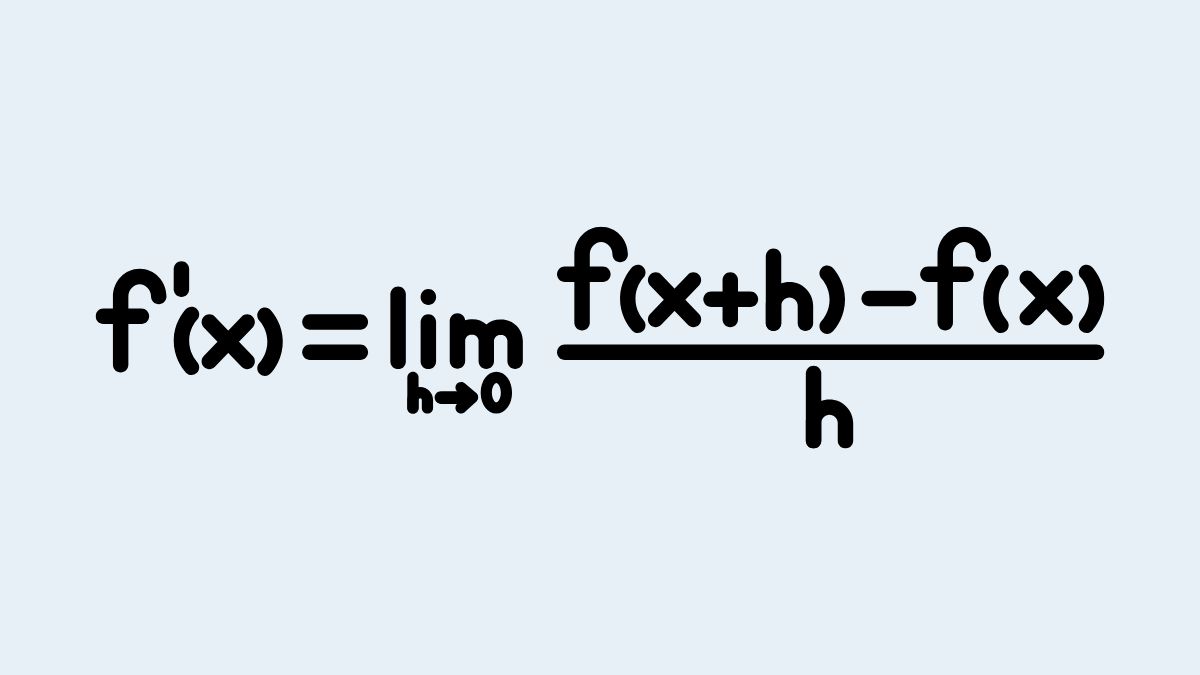
Lũy thừa và đa thức
Nền tảng quan trọng nhất của Công Thức Đạo Hàm là ((xn)’=n x) với (n) hằng số, kéo theo ((c)’=0) và ((ku)’=k u’). Với đa thức, bạn đạo hàm từng hạng rồi cộng lại, đồng thời nhớ số mũ âm yêu cầu (x\neq 0). Ví dụ (f(x)=3x4-2x+5\Rightarrow f'(x)=12x3-2), kết quả ngắn gọn nếu bạn không biến đổi rườm rà.
[(xn)’=n x,\qquad (c)’=0
]
Hàm mũ và logarit
Nhóm mũ–log thường xuất hiện trong bài tăng trưởng và khảo sát: ((ex)’=ex), ((ax)’=ax\ln a) với (a>0,a\neq 1), và ((\ln x)’=\dfrac{1}) trên (x>0). Nếu là (\ln|x|), đạo hàm vẫn là (\dfrac{1}) nhưng miền xác định là (x\neq 0), nên bạn phải ghi điều kiện trước khi xét dấu. Với (\ln(g(x))) hoặc (a^{g(x)}), kết quả luôn kèm thêm nhân (g'(x)) theo dây chuyền.
[(ex)’=ex,\quad (ax)’=ax\ln a,\quad (\ln x)’=\frac{1}
]
Hàm lượng giác
Các công thức “xương sống” là ((\sin x)’=\cos x), ((\cos x)’=-\sin x), ((\tan x)’=\dfrac{1}{\cos2 x}) và ((\cot x)’=-\dfrac{1}{\sin2 x}). Điểm dễ sai nằm ở dấu trừ của ((\cos x)’) và điều kiện xác định của (\tan x,\cot x), vì chúng làm miền xét bị tách thành nhiều khoảng. Khi làm khảo sát, hãy chia miền theo nghiệm của (\sin x) hoặc (\cos x) để tránh kết luận đơn điệu “vượt” qua tiệm cận.
[(\sin x)’=\cos x,\quad (\cos x)’=-\sin x,\quad (\tan x)’=\frac{1}{\cos^2 x}
]
Công Thức Đạo Hàm theo quy tắc biến đổi

Tuyến tính và quy tắc hằng số nhân
Bạn được phép đạo hàm theo từng phần nhờ ((u\pm v)’=u’\pm v’) và ((ku)’=k u’), nên hãy rút gọn biểu thức thành tổng các hạng đơn giản trước khi tính. Cẩn thận với phép biến đổi làm thay đổi miền xác định (ví dụ rút gọn có chia cho biểu thức có thể bằng 0), vì miền của hàm gốc mới là cơ sở để xét dấu. Sau khi có (f'(x)), hãy ghi rõ các điểm loại để bảng biến thiên không bị sai khoảng.
Quy tắc nhân và quy tắc chia
Nếu (y=uv) thì ((uv)’=u’v+uv’), còn nếu (y=\dfrac) thì (\left(\dfrac\right)’=\dfrac{u’v-uv’}{v^2}) với (v\neq 0). Dấu trừ ở tử số là nơi hay nhầm, vì vậy bạn nên đặt ngoặc toàn bộ tử số trước khi bình phương mẫu. Một kiểm tra nhanh là thế thử một giá trị đơn giản để xem đạo hàm có “phi lý” so với độ dốc trực quan hay không.
Quy tắc dây chuyền và hàm hợp
Quy tắc dây chuyền nói rằng nếu (y=f(u)), (u=g(x)) thì (\dfrac=f'(u)\cdot u’), và đây là lý do đa số đáp án có thêm một hệ số “đi kèm” từ ruột. Ví dụ (y=\sqrt{3x2+1}\Rightarrow y’=\dfrac{3x}{\sqrt{3x2+1}}), trong đó (6x) từ ruột quyết định kết quả đúng. Khi biểu thức nhiều lớp, bạn đặt biến trung gian theo từng tầng để không bỏ sót nhân tử.
Hàm ẩn và tham số (nâng cao hay gặp)

Với hàm ẩn (F(x,y)=0), bạn đạo hàm hai vế theo (x) và nhớ (y=y(x)), nên các hạng chứa (y) sẽ sinh thêm (y’) (ví dụ ((y^2)’=2y\cdot y’)). Với tham số (x=x(t)), (y=y(t)), công thức thường dùng là (\dfrac=\dfrac{dy/dt}{dx/dt}) khi (dx/dt\neq 0), rất tiện để tìm tiếp tuyến của đường cong. Điểm quan trọng là luôn kiểm tra điều kiện chia và miền xác định trước khi kết luận.
Cách học, kiểm tra và ứng dụng nhanh
Cách ghi nhớ để không học vẹt
Để học Công Thức Đạo Hàm hiệu quả, bạn hãy gom thành 2 bảng: (1) đạo hàm của các hàm cơ bản, (2) các quy tắc (tuyến tính, tích, thương, dây chuyền). Mỗi lần gặp bài mới, bạn chỉ cần nhận diện nó thuộc “nhóm hàm” nào và “nhóm quy tắc” nào, rồi lắp ghép đúng thứ tự. Luyện 5–10 bài ngắn mỗi ngày sẽ giúp bạn hình thành phản xạ nhanh hơn học dồn.
Tự soát lỗi trong 30 giây
Ba lỗi phổ biến là quên điều kiện xác định, sai dấu ở quy tắc chia và quên nhân đạo hàm của ruột. Bạn có thể soát bằng “dấu hiệu hình thái”: ((\ln g(x))’) luôn có dạng (\dfrac{g'(x)}{g(x)}), còn ((\sqrt{g(x)})’) luôn có mẫu (\sqrt{g(x)}). Nếu kết quả không mang các dấu hiệu này, hãy quay lại bước đặt ruột–vỏ và kiểm tra hệ số khám phá thêm tại xe may anh loc.
Ứng dụng trong cực trị và tiếp tuyến
Trong bài cực trị, bạn giải (f'(x)=0) để tìm điểm tới hạn rồi xét dấu (f'(x)) hoặc dùng (f”(x)) để kết luận. Với tiếp tuyến tại (x_0), hệ số góc là (k=f'(x_0)) và phương trình là (y=f(x_0)+k(x-x_0)), đồng thời (x_0) phải thuộc miền xác định. Khi làm khảo sát, quy trình ổn định nhất là: xác định miền, tính đạo hàm, xét dấu theo từng khoảng, rồi mới kết luận.
Trâm Anh là tác giả chính của trang web Xe Máy Anh Lộc . Với ngòi bút sắc sảo và am hiểu sâu về xe máy, cô chuyên viết review chi tiết, đánh giá xe cũ, hướng dẫn mua bán, tập trung vào các dòng tay ga phổ biến như Honda SH, Air Blade, Liberty. Nội dung thực tế, hữu ích, giúp người đọc đưa ra quyết định sáng suốt.
