Chu vi hình tròn là kiến thức hình học cơ bản nhưng lại xuất hiện rất nhiều trong các bài toán từ tiểu học đến trung học. Khi hiểu rõ khái niệm, công thức và cách vận dụng, bạn sẽ giải bài nhanh hơn và tránh nhầm lẫn với các đại lượng khác như diện tích. Kiến thức này cũng giúp bạn liên hệ với nhiều tình huống thực tế như đo và thiết kế các vật có dạng tròn trong đời sống hằng ngày.
Chu vi hình tròn là gì? Công thức cơ bản cần nhớ
Khái niệm chu vi hình tròn
Trong hình học phẳng, chu vi đường tròn được hiểu là độ dài đường bao quanh toàn bộ hình tròn. Nếu bạn dùng một sợi dây ôm sát quanh một cái đĩa tròn rồi kéo thẳng sợi dây đó ra, chiều dài sợi dây chính là chu vi của đường tròn. Việc nắm chắc khái niệm giúp bạn hiểu công thức thay vì chỉ học thuộc một cách máy móc.
Công thức tính chu vi theo bán kính
Chu vi hình tròn thường được ký hiệu là C và được tính dựa trên bán kính r của đường tròn. Công thức quen thuộc là C = 2 × π × r, trong đó π là số Pi với giá trị xấp xỉ 3,14. Khi nhớ được mối liên hệ giữa chu vi và bán kính, bạn có thể dễ dàng suy ra các đại lượng khác trong bài toán.
Công thức tính chu vi theo đường kính
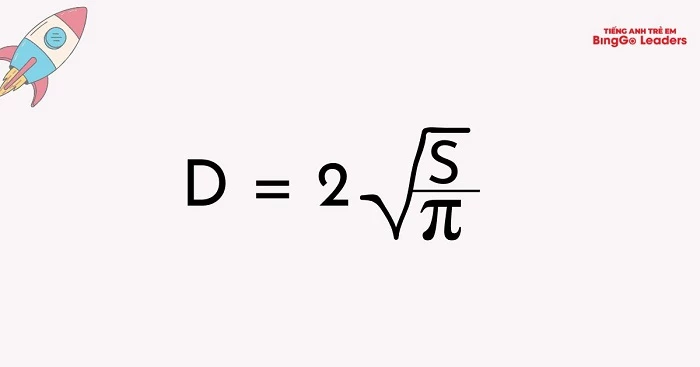
Khi đề bài cho sẵn đường kính d, bạn có thể áp dụng công thức rút gọn là Chu vi hình tròn C = π × d. Nhờ đó, thay vì phải tính bán kính, bạn chỉ cần nhân số Pi với độ dài đường kính là đã có kết quả. Cách viết công thức như vậy giúp bài giải ngắn gọn, dễ trình bày và giảm nguy cơ sai sót khi tính toán.
Chu vi đường tròn và vai trò của số Pi
Số Pi là gì và vì sao quan trọng?
Trong toán học, số Pi (π) là hằng số thể hiện tỉ lệ giữa chu vi và đường kính của mọi đường tròn. Dù bạn vẽ đường tròn lớn hay nhỏ thì khi lấy chu vi chia cho đường kính, kết quả luôn xấp xỉ 3,14159. Nhờ tính chất này, Pi trở thành cầu nối giữa chu vi, đường kính và bán kính giúp các công thức trở nên thống nhất, dễ sử dụng.
Làm tròn số Pi trong bài toán thực tế
Khi giải bài tập ở trường, bạn thường được phép lấy π ≈ 3,14 hoặc π ≈ 3,1416 để tính cho nhanh. Trong một số trường hợp, giáo viên có thể yêu cầu để nguyên π trong kết quả để đảm bảo độ chính xác. Vì vậy, khi làm việc với Chu vi hình tròn, bạn cần đọc kỹ đề bài xem dùng giá trị gần đúng hay giữ nguyên ký hiệu π.
Các dạng bài tập liên quan đến chu vi hình tròn
Dạng bài tính chu vi khi biết bán kính hoặc đường kính
Với dạng bài cơ bản, đề thường cho bán kính hoặc đường kính rồi yêu cầu tính Chu vi hình tròn. Cách làm là bạn xác định đúng dữ kiện, chọn công thức phù hợp C = 2πr hoặc C = πd rồi thay số vào. Khi trình bày, bạn nên viết rõ bước ghi công thức, bước thay số và bước kết luận để bài giải mạch lạc, dễ hiểu.
Dạng bài tính bán kính, đường kính khi biết chu vi
Ngược lại với dạng trên, đề bài có thể cho trước giá trị C và yêu cầu tìm r hoặc d. Khi đó, bạn chỉ cần biến đổi công thức Chu vi hình tròn thành r = C : (2π) hoặc d = C : π. Sau khi tính được bán kính hoặc đường kính, bạn có thể tiếp tục giải các câu hỏi tiếp theo như tính diện tích hoặc so sánh kích thước hai hình tròn.
Những lỗi sai thường gặp khi làm bài
Khi học sinh mới làm quen với chu vi đường tròn, rất dễ nhầm lẫn giữa C = 2πr và S = πr² là công thức diện tích. Một số bạn còn quên nhân 2 với bán kính hoặc quên ghi đơn vị chiều dài trong đáp số. Để hạn chế lỗi, bạn nên ghi chú riêng công thức chu vi, công thức diện tích và đọc lại đề xem bài yêu cầu tính độ dài hay diện tích.
Ứng dụng chu vi đường tròn trong đời sống
Đo độ dài các vật có dạng tròn
Trong thực tế, công thức Chu vi hình tròn giúp bạn ước lượng chiều dài nhiều vật dụng quen thuộc. Chẳng hạn, khi biết đường kính bánh xe đạp, bạn có thể tính chu vi bánh xe để suy ra quãng đường đi được sau mỗi vòng quay. Việc đo chu vi miệng giếng, nắp cống, bàn tròn hay các chi tiết hình tròn trong xây dựng cũng dựa trên nguyên lý chu vi đường tròn cùng với xe máy Anh Lộc.
Mẹo ghi nhớ nhanh công thức chu vi
Để ghi nhớ công thức Chu vi hình tròn, bạn có thể dùng mẹo đọc thành câu “Cờ Hai Pi Rờ” tương ứng C = 2πr. Khi làm quen với cách gọi vui này, bạn sẽ dễ dàng nhớ được chu vi phụ thuộc trực tiếp vào bán kính và số Pi. Bên cạnh đó, việc luyện tập nhiều bài tập từ đơn giản đến nâng cao sẽ giúp bạn thuộc lòng công thức và áp dụng linh hoạt trong mọi dạng bài.
